Introdução:
Você sabia que é possível esquadrejar ângulos retos de forma precisa usando apenas uma trena e o famoso Teorema de Pitágoras? Neste guia simples, vamos explicar como você pode realizar essa tarefa sem a necessidade de equipamentos complicados. Com alguns passos fáceis, você estará pronto para esquadrejar com confiança. Vamos lá!
Passo 1: Entendendo o Teorema de Pitágoras para esquadrejar com trena
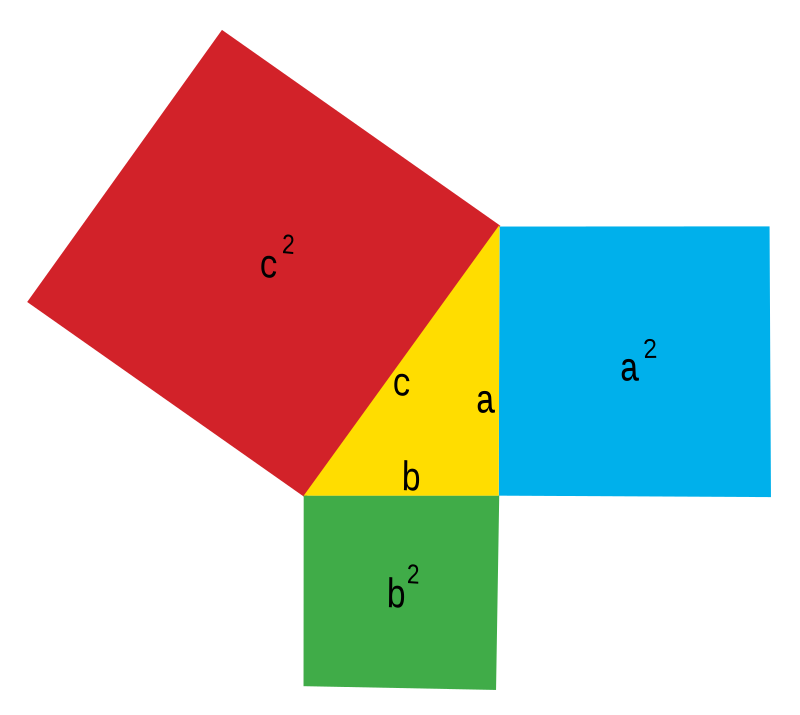
Antes de tudo, é importante compreender o básico do Teorema de Pitágoras. Este teorema afirma que, em um triângulo retângulo, a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa. Em outras palavras, se você tem um triângulo com um ângulo reto (90 graus), pode calcular o comprimento do terceiro lado usando a seguinte fórmula:
c² = a² + b²
Onde:
“c” é o comprimento da hipotenusa (o lado oposto ao ângulo reto).
“a” e “b” são os comprimentos dos catetos (os lados que formam o ângulo reto).
Passo 2: Prepare sua Trena
Certifique-se de que sua trena está limpa, em boas condições e estendida completamente. É importante que ela esteja funcionando corretamente para obter medidas precisas.
Passo 3: Esquadrejando com a Trena
Agora, vamos aplicar o Teorema de Pitágoras para esquadrejar. Suponha que você deseja criar um ângulo reto em um terreno ou em algum projeto de carpintaria. Siga estes passos:
a) Escolha um ponto de referência onde você deseja começar o primeiro lado do ângulo reto (por exemplo, uma parede ou uma estaca no terreno).
b) Use sua trena para medir um determinado comprimento “a” a partir desse ponto e marque-o.
c) A partir do ponto onde você marcou “a”, meça o comprimento “b” em um ângulo reto com o primeiro lado e marque-o.
d) Agora, conecte as duas marcas com a trena para formar o lado da hipotenusa “c”. Certifique-se de que a distância é igual à raiz quadrada da soma dos quadrados de “a” e “b”.
e) Após medir e marcar corretamente, você terá um ângulo reto perfeito!
No exemplo acima apenas a imagem do lado direito está devidamente esquadrejada, pois a soma dos quadrados de 3 e 4 dá 25 que é igual ao quadrado de 5, ou seja, 25.
Ainda na figura acima, o personagem que está do lado do cateto de 4 metros terá que abrir o ângulo até atingir 5 metros na hipotenusa.
Um exemplo prático para esquadrejar com trena
Se você tiver um triângulo com lados de 60 cm e 80 cm, por exemplo, e quiser verificar se ele forma um ângulo reto, aplique o Teorema de Pitágoras:
a² + b² = c²
Onde “a” e “b” são os comprimentos dos catetos (60 cm e 80 cm, respectivamente) e “c” é o comprimento da hipotenusa. Vamos calcular:
60² + 80² = c²
3600 + 6400 = c²
10000 = c²
Agora, calcule a raiz quadrada de 10000:
c = √10000
c = 100 cm
Se a hipotenusa (c) tiver um comprimento de 100 cm, isso significa que os lados de 60 cm e 80 cm formam um ângulo reto, pois 60² + 80² é igual a 100² (Teorema de Pitágoras). Portanto, o triângulo é retângulo.
Conclusão:
Esquadrejar com uma trena e o Teorema de Pitágoras pode parecer complexo, mas seguindo esses passos simples, você será capaz de criar ângulos retos com precisão em seus projetos. Lembre-se de que a prática leva à perfeição, então continue aperfeiçoando suas habilidades e aplicando esse método em suas atividades diárias. Com o tempo, você se tornará um mestre em esquadrejar de forma eficaz e precisa. Boa sorte!